Heap Sort | Pseudo Code | Example | Analyzing Complexity

In this blog post we’ll introduce you to a very beautify sorting algorithm called Heap sort. We have already discussed Insertion Sort and Merge Sort . Heap sort tries to combine the best of both of those algorithms. Like merge sort but unlike insertion sort the complexity of the algorithm is O(n*lgn) where lgn is log base 2. Like insertion sort but unlike merge sort it takes a fix number of elements to be sorted at a particular time.

Moreover, in this blog post we will be going through a new data structure called ‘heap’. The term heap is used in heap sort algorithm although it has been used for garbage collection method in object oriented programming language like java and c++. In this blog post we will be looking at heap in heap sort algorithm.

So, in this blog post we are going to cover the following topics:

• Introduction to heap, max-heap, min-heap
• Maintaining the heap property and building heap
• Heap sort algorithm
• Analyzing the complexity of heap sort algorithm

So, let’s start with introduction to heap, max-heap, min-heap

Heap is a data structure mapped from an array that must be a complete binary tree (meaning there shouldn’t be any missing child nodes). Each node on the tree should corresponds to the array element.

Tree is completely filled at all levels except possibly the lowest. Array represents heap with two arrtributes:

A.length : length of the array

A.heap-size: Numbers of elements in the heap are stored in the array

Where 0 <= A.heap-size <= A.length are valid elements of the heap. The root of the tree is A[1] and given the indexes of the node, we can easily compute the indices of its parent, left child and right child

Given the index of the element, we can find the parent element, left and right element of index using following algorithm :

Let us consider the following example:

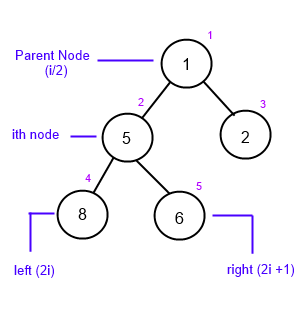
We are given a heap where we take the ith element as 5 (as seen in position 2 of the heap). Parent node will be at position 1 as (2/2 = 1) and left node will be at (2i) position i.e at (2*2=4) 4^th position and right node will be at (2i+1)position i.e (2*2 + 1)position i.e at 5^th position.

Now we have a basic understating of heaps. There are two types of heaps we will be using in our blog: max-heap and min-heap. A heap in which the parent element is greater than both the child elements is a max-heap and a heap in which the parent element is less than both the child elements is a min heap.

A[parent] >=A[i] i.e max heap

A[i]>= A[parent] i.e. min heap

In min heap the smallest element is the root element and at max heap the largest element is the root element.

For the heap sort algorithm we use max-heap. Viewing heap as tree we define the height of the heap to be the number of edges on the longest simple downward path from the node to the leaf. Since a heap of n elements is based on a complete binary tree, its height theta of lgn time or simply (h).

Maintaining the heap property

In order to maintain the max-heap property, we use Max-heap algorithm. It takes input as array and index of the array. Max-heapify is recursively called till the lowest element reached the bottom of the tree or at the last index of the array. Let us consider the following algorithm:

The above algorithm gives a basic knowledge of how max-heapify works. We are given A[i],A[left] and A[right], we need to find the maximum of the three values. If array value at ith position is largest of three values, we don’t need to change the values since max value is at the root. If array value at the right or left position is largest, then we need to exchange the value since we want the max value to be at the root of the heap in max-heap.

Building the heap

In order to convert an array into max-heap, we will be using bottom to up approach taking array as the parameter input. The algorithm is given as follow:

In the above algorithm we parse from (A.length/2) because we want to parse only the parent elements having child nodes. Every time it parses the parent element it calls the MaxHeapify function and reorders the heap till the time it follows the max-heap property.

We will be using the above algorithm with example after we have a look at heapsort algorithm, which will make it easy for us to understand the algorithm.

Heapsort Algorithm

In the above algorithm, we will first build the max-heap from the given array. Next we parse the array from the array size till 2 which is the second element of the array. Once we get only one element remaining in the array heap, we don’t need to parse it further. But till the time we have more than 1 element in the array, we will take the last element of the array and exchange it with the first element since in a max-heap the largest element is at the root node and build the max heap of the array. This process will continue till we get all the element in the array sorted.

Let us consider the following example

Once we are given the array of unsorted numbers, we first create a heap out of it. Once we have the heap we then follow MaxHeapify to obtain the max value and store it at the last position of the array by exchanging it with the element at the first position and place it into a different array called the sorted array. We will continue this process till only one element is present in the array. Once one element is present and we have all the sorted element in the other array we have our sorted array.

Analyzing the complexity of Heap sort algorithm

Heap sort algorithm uses two main function BuildMaxHeap and MaxHeapify. The first one has a complexity of O(n) and MaxHeapify has a complexity of O(lgn) which goes from A.length downto 2, having the final complexity as (n-1)*lgn.

Final complexity = O(n) + O((n-1)*lgn)

= O(n) + O(nlgn) – O(lgn)

= O(nlgn) which is the complexity of heap sort algorithm.

That’s all folks ! We are done with heap sort algorithm, we understood what heaps are, how to build a max-heap and use it in heap sort algorithm. We even took an example explaining the algorithm.